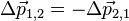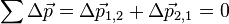Força é um dos conceitos fundamentais da Física newtoniana. Relacionado com as três leis de Newton, é uma grandeza que tem a capacidade de vencer a inércia de um corpo, modificando-lhe a velocidade (seja na sua magnitude ou direção, já que se trata de umvetor). Como corolário, chega-se ao constructo de que a força pode causar deformação em um objeto flexívelCitação: Força: qualquer agente externo que modifica o movimento de um corpo livre ou causa deformação num corpo fixo. Intuitivamente, a força se identifica com as noções de empuxo ou impuxo. A força, por ser também um vetor, tem dois elementos: amagnitude e a direção. A Segunda Lei de Newton , foi originalmente formulada em termos ligeiramente diferentes, mas equivalentes: a versão original afirma que a força que age sobre um objeto é igual à derivada temporal do momento linear deste objeto.
Alguns conceitos relacionados com a força:
- pressão, divisão ou distribuição da força sobre a área;
- arrasto, diminuição da velocidade de um objeto;
- torque, momento que produz mudanças na velocidade de rotação de um objeto.
A força aplicada num corpo fixo é chamada tensão mecânica ou estresse mecânico, um termo técnico para as influências que causam deformação da matéria. Enquanto o estresse mecânico pode permanecer incorporado em um objeto sólido, gradualmente, deformá-lo, estresse mecânico em um fluido determina mudanças em sua pressão e volume.
A moderna versão da segunda lei de Newton é uma equação diferencial:
Em um sistema de massa constante, o uso da regra da constante na diferenciação permite que a variável massa seja recolocada fora do operador diferencial; assim, chega-se a:

Por substituição da definição da aceleração, chega-se, finalmente, à versão algébrica da segunda lei de Newton:
Algumas fontes chamam esta lei de "segunda fórmula mais famosa da física", perdendo apenas para a E=mc2 de Einstein.Newton jamais enunciou explicitamente a lei nesta forma reduzida.
A segunda lei de Newton afirma a proporcionalidade direta de aceleração à força (no caso da massa constante) e a proporcionalidade inversa da aceleração à massa (no caso de força constante). A aceleração pode ser definida em dinâmica como a derivada da velocidade em relação ao tempo. No entanto, em física avançada, ainda há questões profundas que permanecem, como em relação à definição adequada da massa.
O conceito de relatividade geral oferece uma equivalência entre espaço-tempo e massa, mas algumas fontes citam a segunda lei de Newton como definição de massa. De outro modo, fontes citam esta mesma lei como definição de força, o que é negado por autores mais rigorosos.
[editar]Terceira Lei de Newton
A Terceira Lei de Newton trata da aplicação simétrica de forças em diferentes objetos. A terceira lei explica que todas estas forças são interações entre diferentes corpos e que entre estes não há uma força unidirecional atuando um único corpo. Sempre que um primeiro exerce uma força F em um segundo corpo, o segundo corpo exerce uma força no primeiro corpo, igual em magnitude e contrária em direção. Esta lei é também referida como lei de ação e reação, sendo que uma força é chamada de ação e a outra de reação. A ação e a reação são simultantêas:
Se o objeto 1 e o objeto 2 são considerados como partes de um sistema, a soma das forças entre objetos do sistema é nula:

No caso de um sitema fechado de particulas em que não há uma força externa, os objetos constituintes podem acelerar-se um em relação ao outro, mas o sistema completo permanece não acelerado, tendo como base de localização o centro de gravidade. Alternativamente, se uma força externa atua sobre o sistema, então o centro de gravidade experimentará uma aceleração proporcional à magnitude da força externa dividida pela massa do sistema.
Combinando a segunda e a terceira lei de newton, chega-se ao resultado da conservação de momento linear de um sitema:

e, aplicando a integral em relação ao tempo, a igualdade:
é obtida. Num sistema que contém os objetos 1 e 2,
(conservação de um momento linear).
Partindo-se da lei e aplicando deduções, cheaga-se a uma generalização para um sistema com vários objetos. Neste caso, ainda, a troca forças entre objetos constituintes não afeta o impulso do sistema como um todo.

 um
um  uma força. Ambos são grandezas vetoriais.
uma força. Ambos são grandezas vetoriais.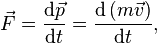 sendo m uma massa e
sendo m uma massa e  sua
sua